Explique cómo se mueven los puntos de una cuerda sujeta por sus extremos en la que se ha formado una onda estacionaria.
Respuesta para Selectividad PAU
Tienen distintas formas de vibrar:
λ = 2L/N (n = 1, 2, 3, …)
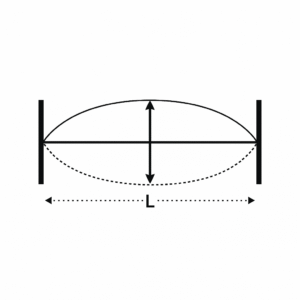
Modo fundamental (n = 1): λ = 2L

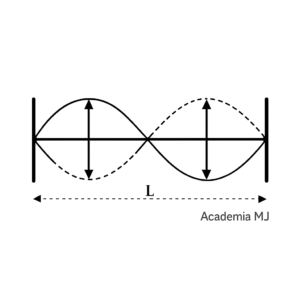
Primer armónico (n = 2): λ = L

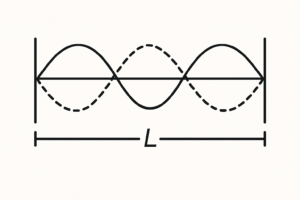
Segundo armónico (n = 3): λ = 2L/3

Principio de superposición y nodos/vientres
En una onda estacionaria sobre una cuerda con extremos fijos se superponen dos ondas viajeras iguales en sentido contrario. Aparecen nodos (puntos inmóviles) y vientres (puntos con máxima amplitud).
Movimiento en nodos y vientres
Los nodos permanecen en reposo permanente. En los vientres, cada punto oscila armónicamente con amplitud máxima A y frecuencia f, describiendo un movimiento vertical de tipo simple.
Ecuación de desplazamiento
y(x,t) = A·sin(kx)·cos(ωt)
Distribución espacial de nodos
Los nodos se encuentran en x = n·λ/2 (n = 0,1,2,…). Entre ellos hay vientres en x = (2n+1)·λ/4. La distancia entre dos nodos contiguos es λ/2.
Implicaciones para Selectividad
Identifica nodos y vientres en gráficos y calcula posiciones de los extremos fijos.
Preguntas frecuentes
¿Qué es un nodo en una onda estacionaria?
Es un punto fijo de la cuerda que no se mueve porque la superposición de las dos ondas produce desplazamiento cero.
¿Dónde se sitúan los vientres?
En puntos de máxima amplitud, localizados a λ/4, 3λ/4, etc., desde uno de los extremos fijos.
¿Cómo varía el desplazamiento en función de x y t?
Según y(x,t)=A·sin(kx)·cos(ωt), donde sin(kx) fija la forma espacial y cos(ωt) la temporal.
¿Qué ocurre en los extremos de la cuerda?
Los extremos fijos son siempre nodos (y=0 en todo instante).
¿Cómo se relaciona el número de modos con la longitud de la cuerda?
El n-ésimo modo tiene n vientres y n+1 nodos, con λ_n =2L/n.
¿Cómo aparece esta pregunta en Selectividad?
Piden graficar y describir movimiento de distintos puntos, calcular posiciones de nodos o frecuencias de resonancia.